Esses engenheiros fantásticos e suas calculadoras maravilhosas

A quantidade de coisas que acabamos por descobrir nessa era de blogs, comunidades virtuais e listas de discussão é realmente impressionante. Se, há meros 10 anos, um professor de uma universidade estadual brasileira qualquer, situada em uma cidade interiorana qualquer, publicasse uma curta nota em um jornal local afirmando ter descoberto um erro no cálculo de uma importante quantidade matemática, pessoas como eu, que moram a centenas de quilômetros de distância, dificilmente ficariam sabendo. E é precisamente isso que faz o engenheiro e professor Carlos Pereira de Novaes, da Universidade Estadual de Feira de Santana , que diz ter descoberto um erro no cálculo do número e, a base dos logaritmos naturais e freqüentemente denominado "constante de Napier" ou "número de Euler". Nessa era da internet, contudo, a notícia nos chega por e-mail e podemos perder com ela algum tempo de um fim de semana
No curto artigo em questão, intitulado "Professor da Uefs verifica erro em simbologia matemática" (*), o professor inicia com a definição mais conhecida do número de Euler, dada pela seguinte equação:

A seguir, o autor, pedindo desculpas a Euler (**), afirma ter usado uma calculadora eletrônica para estimar o limite, tendo obtido, não o número 2,71828182846, mas sim o número 1.

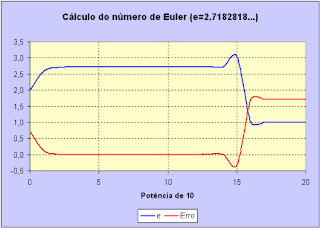
Imediatamente após ler o artigo, abri uma planilha eletrônica e fiz alguns cálculos. Para x maior do que 10⁷ e menor do que 10¹¹, o resultado é dado pela planilha com erro de 10^-7. Acima de 10¹¹, o erro começa a aumentar até que o resultado se torna unitário a partir de 10¹⁶. O que percebemos é que, obviamente, a planilha calcula inicialmente o número (1+1/x), e depois o eleva a x. Para x>10¹⁶, o resultado para 1/x é tão pequeno que a planilha simplesmente o arredonda para zero, obtendo-se e=1, pois o número 1 elevado a qualquer número é também igual a 1. O gráfico da evolução do erro de cálculo de acordo com o aumento de x é ilustrado a seguir.

O autor faz então a ressalva de que o resultado é esse mesmo e que o número (1+1/x) deve ser calculado antes de ser elevado a x. Se isso fosse verdade, a questão não seria simplesmente de “simbologia”, mas sim de uma verdadeira revolução na matemática, com reflexos na física, química e também na engenharia. Só para começar, muita coisa que os estudantes de engenharia elétrica aprendem sobre circuitos elétricos estaria simplesmente errada!

O autor diz ter usado uma calculadora científica HP para obter seus resultados. Infelizmente, tenho apenas uma Casio fx-82TL, que realmente fornece e=1 para a equação (1) e com x>10¹⁶. Coisas da vida.

Evidentemente, existem métodos matematicamente formais para se demonstrar a validade da equação (1), mas engenheiros preferem verificações numéricas a demonstrações analíticas. Mas como contornar as limitações de planilhas e calculadoras eletrônicas, sem recorrer a complicados pacotes numéricos?

Uma possibilidade é desenvolver um programa de computador que faça o cálculo com precisão maior do que uma calculadora ou planilha eletrônica. O Turbo Pascal, por exemplo, dispõe de variáveis reais de precisão estendida (extended), que constituem em números com mais de 400 casas decimais. Usando a função Power do Pascal, implementada no Turbo Delphi Explorer, escrevi então um pequeno programa para calcular o número de Euler. A situação melhorou, mas não muito. Em vez dos cálculos entrarem em colapso para x>10¹¹, o colapso ocorreu para x>10¹⁴, quando o erro se tornou maior do que 10^-6. Nem mesmo as variáveis extended resistem a cálculos com esses números enormes (é verdade que usei um laptop com um modesto processador Celeron de 1,5 GHz).

Pensei então em contornar as limitações da função Power usando um processo iterativo: calcula-se inicialmente o número (1+1/x), multiplicando-se o resultado por ele mesmo x vezes. O processo funcionou admiravelmente bem, com um pequeno detalhe: para números realmente grandes, digamos x>10²⁰, os testes indicam que o processamento demoraria alguns dias, talvez anos. Esse é o problema com limites com variáveis tendendo ao infinito: eles demoram uma eternidade para serem testados! Para manter o tempo de processamento inferior a 40 minutos, por exemplo, o valor máximo de x deve ser 10¹¹.

Mas, como diz o velho ditado matemático, “quando você não puder vencer, trapaceie”. Após quebrar a cabeça por algum tempo, descobri que “trapaça”, nesse caso, consiste em realizar as iterações de maneira recursiva. Primeiro multiplicamos (1+1/x) por ele mesmo, obtendo (1+1/x)². A seguir, multiplicamos (1+1/x)² por ele mesmo, obtendo (1+1/x)⁴ e assim por diante. Esse método implica em que o número x deve ser da forma x=2ⁿ, onde n é o número de iterações. O número 2 aparece porque os fatores de uma iteração, são multiplicados aos pares.

Usando o método de iterações recursivas, foi possível reduzir o número de iterações para apenas 63, realizadas em menos de um milisegundo e não em algumas décadas. O valor correspondente de x é 2⁶³=9,22x10¹⁸, ou aproximadamente 10¹⁹, uma melhoria de pelo menos 1.000 vezes em relação aos métodos anteriores.

Para n>64, infelizmente, o método entra em colapso novamente e o resultado torna-se unitário. Contudo, o uso de métodos computacionais progressivamente mais sofisticados, com resultados condizentes para e, deixa claro que o problema em questão diz respeito às limitações computacionais existentes, e não a qualquer problema com a definição do número de Euler.

O programa executável, o respectivo código-fonte em Turbo Delphi Explorer e a planilha que usei para fazer alguns cálculos estão disponíveis em http://www.daelt.sh06.com/profs/alvaug/Euler.zip. É só verificar.

É claro que mesmo o número 10¹⁹ ainda está tão longe do infinito quanto o número 10, e nenhum matemático que se preze aceitaria verificações numéricas como prova de um teorema. Felizmente, há outras definições para o número de Euler, tais como a que se segue, baseada na expansão da função exponencial em série de McLaurin:

onde x! é o fatorial de x. Inserindo essa definição em uma planilha eletrônica, obtemos resultados com erro decrescente até que, em x=16, o erro se anula, obtemos o valor correto para o número de Euler e o grande matemático pode descansar em paz. O problema certamente está na maneira como os computadores tratam números muito pequenos em algumas situações, mas não em outras.

O problema levantado pelo professor Novaes e a reação a ele deixam algumas lições, a primeira delas dirigida especialmente aos alunos de engenharia de todos os tempos e lugares:

• Não confie demais na sua HP.


• Quando um pesquisador independente afirma ter descoberto provas de que um resultado conhecido há séculos, testado e comprovado pelas mais diversas pessoas nos mais diversos lugares, está errado, é muito provável que este pesquisador esteja enganado. Contudo, ele jamais se convencerá disso.


• Quando confrontados com a contestação de um resultado conhecido há séculos, publicada por um pesquisador independente, a maioria dos profissionais de qualquer área responderá com argumentos pessoais, visando desqualificar o pesquisador em vez de contestar os argumentos dele.


• Antes de publicar seus resultados revolucionários, envie-os para ser revisado por profissionais da área. Isso diminuirá o constrangimento e possíveis ameaças de
  morte. Coisas da vida.

(*) O artigo original, publicado em http://www.uefs.br/portal/news/2007/professor-da-uefs-verifica-erro-em-simbologia-matematica, foi removido, mas continua disponível em http://www.universiabrasil.net/noticia/materia_dentrodocampus.jsp?not=35247. O assunto também está em discussão em algumas comunidades do Orkut, tais como http://www.orkut.com/CommMsgs.aspx?cmm=68052&tid=2511957267834183215.
(**) Não é necessário pedir desculpas a Euler. O número e foi introduzido pelo matemático John Napier e a equação (1) foi estudada pelo matemático Jacob Bernoulli. Tudo o que Euler fez, nesse caso, foi introduzir a notação e (de “exponencial”), em sua obra Mechanica, de 1736.